So it turns out that I'm not that crazy, and my formula for the probability of finding prime numbers is a special case of the Euler Product. It turns out this Euler Product is deeply related to Riemann's Zeta Function!!!
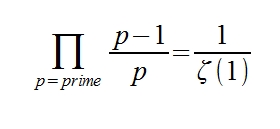
Here is the proof on Wikipedia:
Euler's proof is actually very straight forward and easy to understand. Don't be afraid to read it.
I figured if there is a Zeta Function associated with my prime product, isn't there one for my twin prime product? And it turns out there is one that an anonymous helped me find. But first, let's look at one thing that occurs with the twin prime product that does not with the Euler Product:
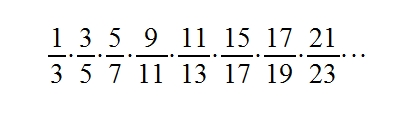
Notice how half of the twin primes cancel each other out. My idea is to find how this cancelling out of half of the twin primes manifests itself in the Zeta form of this product. Here is the Zeta form of my twin prime product:
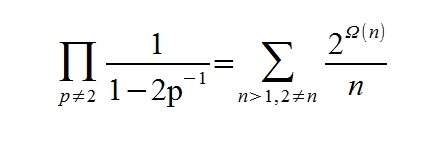
Where Ω(n) is the number of prime factors of n (counted with multiplicities), and where the product on the left ranges over all prime numbers p, and the sum on the right ranges over all positive odd integers n.
You can quickly verify that the product on the left is the inverse of my twin prime product.
So...
Is there any way to see how this cancelling out of twin primes in the product on the left manifests itself in the infinite sum on the right?
If you know the answer you may have stumbled onto something great...