I created this tab mostly for myself to use as a sort of electronic notepad. Some of the properties of prime numbers I've encountered are interesting and you may like them.
Given the following number:
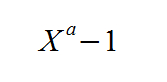
Where "X" is any real number, and where "a" is any other real number.
I've found that when you input this formula in an excel spreadsheet an evident pattern emerges:
- "X" can never be an odd number because the formula will spit out an even number, which can never be prime (except for 2).
- "a" must at least be an odd number, here's why:
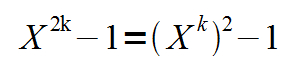
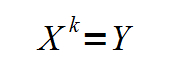
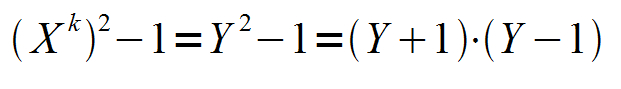
This shows that any number elevated to any even power "2k" and then minus "1", will always have at least 4 factors, and therefore is never prime.
- If I'm not mistaken, "X" can only be an even number that ends in "2" or "8", such as 2, 8, 12, 18, 22, 28... and so on. This comes from a pattern I saw in the excel spreadsheet for how the last digit behaves in the output of the first formula on this tab (WEIRD!).
Mersenne Primes are of the form:
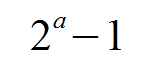
- Mersenne primes can only end in "1" or "7". This is because the pattern for "2" to the power of "a" using only consecutive odd numbers for "a" spits out results with the last digit ending as follows: 8, 2, 8, 2, 8, 2, 8, 2, 8, 2 ... and so on. When you subtract 1 from this result you either get a 1 or a 7 in the last digit. Trivial maybe, but I didn't know this until I saw it on the spreadsheet.
I'm hoping my notes grow and I can put some more puzzle pieces together. I leave it up to you, the reader, to explore these patterns in your own spreadsheet. I will post my spreadsheet if someone requests it, but mainly it is a lot of number mumbo jumbo which is not pretty to look at, but the patterns are there, it's just a matter of knowing how to see them.