Primal Chaos (Visualizations)

 By: Carlos Paris

e-mail: carluchoparis (at) yahoo (dot) com

A special thanks to Infosthetics and Vizworld as well as other bloggers for posting my story and directing traffic to my site!

http://infosthetics.com/archives/2009/12/visualizing_prime_numbers.html

http://www.vizworld.com/2009/12/visualizing-prime-numbers-primal-chaos/

In the words of Friedrich Nietzsche “When you stare at the Abyss, the Abyss stares back at you”. When I stared at my computer screen and realized what I was seeing, I felt something stare back at me. It might have been the beauty of the image, or the smiley face on my Facebook page.

It had been a regular day at work. I pushed throughout the day working in Autocad drawings to meet a deadline for an HVAC system design project. At 5:30 pm, when all plans were signed and sealed, and all quality control work was done for the n^th time, I went home.

I gave my wife Johanna a kiss and took my 2 children Christopher and Anabella to the backyard to play around for a while. Florida weather in mid to late November is usually pretty nice so this is a refreshing part of the day, and as any parent knows, it takes work and love to spend quality time with your kids before they go to bed. Once the kids are in bed you actually have time to think and ponder your life.

With Christopher and Anabella sleeping, I powered on my self-assembled computer, and started looking at Yahoo News. One of the headlines was about a big $$$ prize for whoever finds the biggest prime number yet. I've always had a passion for mathematics and physics, which are hobbies I've always balanced out with my professional and personal life, so this news story was of interest to me, and it read something like this:

“A prize of One Million Dollars is offered to whoever finds the biggest prime number up to 1 Billion DIGITS.”

You may have noticed the word “Digits” is in capitals and bold. This is the key word I did NOT see! I thought it was up to the number 1 billion which only has 10 digits!!! I was however very motivated to ponder about prime numbers for a couple of hours. I kept thinking “1 million bucks, 1 million bucks!” I did not know what I was getting myself into...

The first question you may have is “What are prime numbers?”. They are numbers which are only divisible by themselves and the number one. These numbers have only two factors. For example, the number 15 can be divided by 1, 3, 5 & 15, so it has 4 factors, but the number 17 can only be divided by 1 & 17, so it has only 2 factors, which makes 17 a prime number. These numbers are the most important objects in mathematics because, as the ancient Greeks discovered, they are the building blocks of all numbers—any of which can be broken down into a product of primes. (For example, 105 = 3 x 5 x 7.) They are the atoms of arithmetic, and I now know they also represent one of the greatest challenges in mathematics.

I had known most of my life about prime numbers, but never thought much about them. That night, I started to scribble some formulas and draw random geometrical shapes that took me nowhere. But, being an HVAC Mechanical Engineer, I took this exploration to the next level by firing up Autocad (which is what I use for developing HVAC System Construction Documents).

The first thing I did was draw 32.000 consecutive circles of diameter equal to 1 unit, so each consecutive circle represents every consecutive integer from zero to 32.000. Every single circle in this series represents a multiple of 1.

Next, below the family of circles of diameter 1, I input 16.000 consecutive circles of diameter 2. Every circle in this family represents a multiple of 2.

Next, I applied the same procedure to circles of diameters 3, 4, 5, and so on. Each family of new circles aligned vertically with all previous circles. The resulting image is Figure 1:

Figure 1 

 I started pondering about how all these consecutive circles fit into others of different sizes. It is visually very difficult to see with this image, so to solve the issue, I merged all these series of circles on top of each other at a common origin. The resulting image is Figure 2:

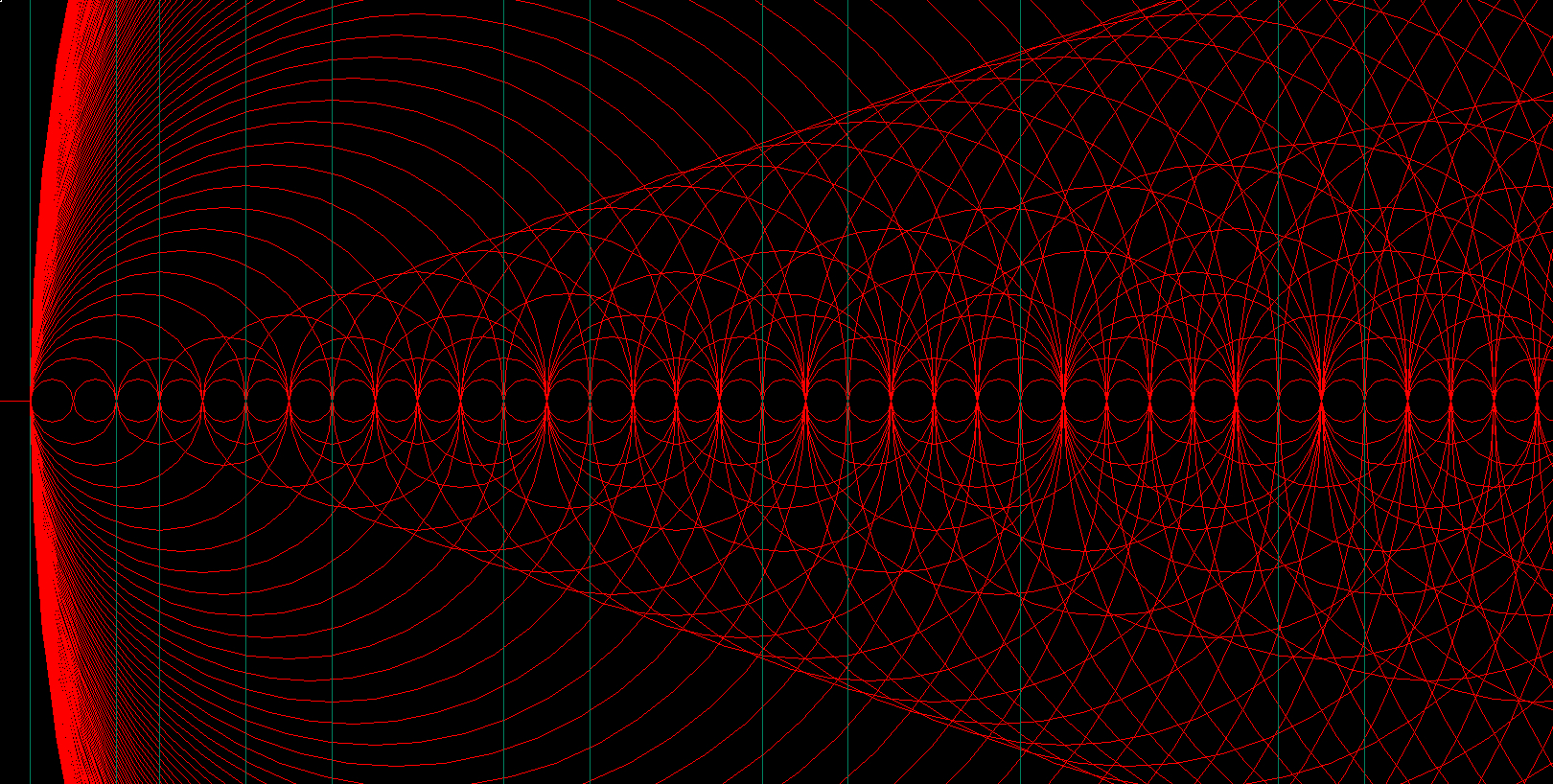
 Figure 2

Developing Figure 2 for the first few circles took me a few minutes, but that was more than enough. When I saw the pattern, it just exploded in my face. It is orderly chaos! That's when I felt something from beyond the screen staring back at me. The patterns and shapes generated above never repeat, they always look different depending on your location to the right of the origin. And most importantly, now you can visually tell how all circles fit into each other! I call the image a “Map of Factors” because it tells you all the factors for each number. Wherever you have only 2 circles intersecting the horizontal axis at their right quadrants, you have a prime number! The green vertical lines show the locations of the prime numbers.

Figure 3 zooms out a bit and shows us more information:

 Figure 3

Please note that in order to discern factors up to 200 for example, we would only have to input consecutive circles of diameters between 1 and 100. This is because any number larger than 100 will not fit into 200 by definition, therefore we only need to input families of circles up to a diameter equal to ½ of the number we want to probe for factors.

Figure 4 

How far can this "Map of Factors" actually take us, you may ask. Well, here's my reasoning behind it: suppose you grab any number "n", and divide it by 3. If the number is divisible by 3, then it is also divisible by the result of that division. For example, if 18 is divisible by 3, then it is also divisible by 6, which is the result of 18/3. Now let's do this for a prime number "p", if "p" is NOT divisible by 3, then it is not divisible by the result of that division rounded up or down to the nearest integer either. Next, if "p" is not divisible by 5, then it is not divisible by the result of that division rounded up or down to the nearest integer either. If we keep going using 7, 9, 11, 13, and so on, at some point the divisor and the result of the division will actually meet, when that happens you're right at the square root of "p" give or take decimals. Once we have reached this point, there is no need to go on because we would be repeating all the same numbers.

With this reasoning as a weapon, I would be willing to bet that with 101 different and consecutive circle diameters I can get prime numbers up to 101^2 (10201).

Figure 4.1 shows the prime numbers given by the Map of Factors, as input thus far, between the numbers 9700 and 9800. They are right on the money!!! The only difference is that now we are looking for the points where only the circle of diameter 1 intersects the horizontal axis, remember we have not input circles of diameters between 9700 and 9800. There is no specific reason why I chose this interval. It was actually just kind of randomly chosen. Please note that the numbers 9700 and 9800 are obviously not prime numbers.

Figure 4.1 

I have created a couple of animations that depict the map of factors as it changes along the horizontal axis. Some of the patterns that emerge give the illusion that the image has depth, as if you were looking at an animation of a 3D object.

These Maps of Factors are intriguing because they visually tell us that, since factors are orderly disordered in the numbers axis, then prime numbers are orderly disordered as well. The way the Map of Factors is developed is actually a simple recursion process for circles, but it produces a complex and astonishing image. An image that requires absolutely all circles up to “n/2” where “n” is the point we want to probe for factors. I believe this is what makes Prime Numbers so elusive! There are no defined initial conditions that give them away! Their initial conditions are dependent on where the number is located on the map, so for different numbers, initial conditions are also different. Prime Numbers seem to possess an uncertainty principle that only allows for their probing as far as our computing power permits.

The following video is the one I will send in a coded message to space so that ET knows we're down here! it's just a cool video:

The journey with primes does not end here. We can analyze this Map of Factors to look for hidden patterns. The first one that jumps out is what I call "Cones". Figure 5 highlights these cones in bright green:

 Figure 5

These cones have an equation that defines their angle with respect to the horizontal axis based on a "k" iteration corresponding to each cone:

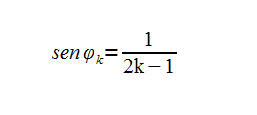
Now, when you analyze the Map for the types of circles that are tangent to each cone, you realize that cones corresponding to even values of k ( k=2, 4, 6, 8... and so on) the corresponding tangent circles always fall onto even numbers on the horizontal axis. If we are looking only for prime numbers and not for factors in general, then we really do not need to have even numbers in our map of factors. That is because prime numbers are odd by definition (all even numbers can be divided by 2 so they have at least 3 factors). So we can basically create an incomplete Map of Factors that would still give away all prime numbers.

The simplest way to do this is keeping circles of diameters 1 and 2 (for visualization purposes), and then start from scratch and input circles of diameters 3, 5, 7, 9, and so on for all odd numbers, but with one catch! they will not be consecutive! they need to always skip 1 circle. The reason is, when you put the second circle for 3, it falls on 6 which is an even number we don't need, so we skip it, and we go to the next one which falls on 9. Same applies for 5, 7, 9, etc.

Figure 6 shows what the map starts to look like:

Figure 6 

The reason I mention this is because it takes 1/4 of the time to build a visual map to find prime numbers, and the size of the file in Megabytes is reduced considerably. The full Map of Factors is much more interesting, because it contains the whole picture, however, the reasoning behind reducing the amount of information without affecting our search for primes is very valuable. As you will later see, when creating an excel spreadsheet that mimics the Map of Factors, and a computer program that verifies if a number, or a set of numbers are prime, we need to use the least amount of information possible in order to improve the efficiency of the programs.

You may also be wondering the reason why I mentioned the equation for the angle of the cones. Well, as you will now see, this equation is very useful for creating a map of factors using only straight lines!

What we're going to do now is draw more lines to see another pattern. The lines will begin at all intersections between the circles and their corresponding cones, and terminate at the intersection of that circle with the horizontal axis as shown on Figure 7:

Figure 7 

It can be easily discerned that each family of lines of the same color have the same angle with respect to the horizontal axis, and lines in each family are offset from each other by a constant number. There is a relation of the angles of these lines and the angle of their corresponding cones. This relation is expressed as follows:

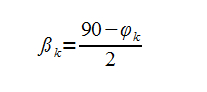
Now, keep in mind I'm drawing all this in Autocad, so for me it is very useful to know the perpendicular offset distance between lines because I can draw a vertical line, then create an array of that line with the corresponding offset distance up to whatever number of lines I want, and then I rotate the family of lines to the corresponding angle required. The perpendicular offset distance can be expressed as follows:

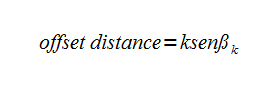
Now that we have a method for drawing a Map of Factors using straight lines, we can go ahead and look at the resulting images. Figure 8 is near the origin,  as you can observe the prime numbers are given away by the locations where no lines intersect the horizontal axis. For example, the subtle vertical line I added on the last circle to the right corresponds to the prime number 47. Note that I have kept circles of diameter "2" in order to more easily know where a prime number can occur (prime numbers will always fall in the centers of these circles).

 Figure 8

Figure 9 zooms out to better visualize what is happening to the families of lines: 

Figure 9 

Each new family of lines crosses the horizontal axis with its first line 2 units further to the right than for the previous family of lines. Additionally, the angle of each family of lines with respect to the horizontal axis as well as the offset distance between lines increases from one family to the next.

Now, a lot of you engineers, business grads, and especially mathematicians, will wonder how to convert this into a numerical program for prime numbers. I built my own computer, but I did not have the chance to purchase Microsoft Office while working on this. Nevertheless, I was able to develop in my mind an Excel Spreadsheet that mimics the map of factors as follows:

1. Input the number 1 into the first cell “A1” (first row and first column) and continue to the right with consecutive numbers.

2. Input the number 2 into the cell “B2” (second row and second column) and continue to the right with the number 2 at every 2 columns.

3. Input the number 3 into the cell “C3” ( third row and third column) and continue to the right with the number 3 at every 3 columns.

4. Continue the input of data for the numbers 4, 5, 6, etc...

5. Input a counter at the bottom of the spreadsheet that will show the number in the first row of that column when there are only 2 numbers in that entire column.

6. The numbers shown at the bottom of the spreadsheet will inevitably be prime numbers.

I called my dad "Eduardo Paris" (http://www.eduardoparis.com/), who has Microsoft Excel by the way, and explained what I had done and how to develop the excel spreadsheet. He quickly developed it and sent me the file. I was able to see the spreadsheet in my own computer once I downloaded OpenOffice for Windows, which is a freeware alternative to Microsoft Office. Here is the spreadsheet:

Also, here's a program created by my dad on Access, after months we realized that it can be made to run a lot faster applying some concepts learned from the sieves, but here it is anyways: