I'd like to first point out that I started this quest for prime numbers hoping for a million bucks. It is implicitly clear in the home tab that I'm no longer in this for the money, I'm just in it for the ride!
We all make mistakes in our life journey that produce unintended consequences. One of my mistakes was confusing a number of 10 digits with a number of 1 billion digits. I'm glad I made this mistake, it helped me explore prime numbers through the eyes of a child.
Anyways, I was never too attracted to the concept of counting prime numbers, but it was inevitable. There is a well known approximation for this which was first discovered by Gauss, but I won't discuss that here, at least not yet. I will only discuss how I first approached the issue.
Let's go back to our famous map of factors showing only multiples of 1, 2 & 3 (Figure 1):
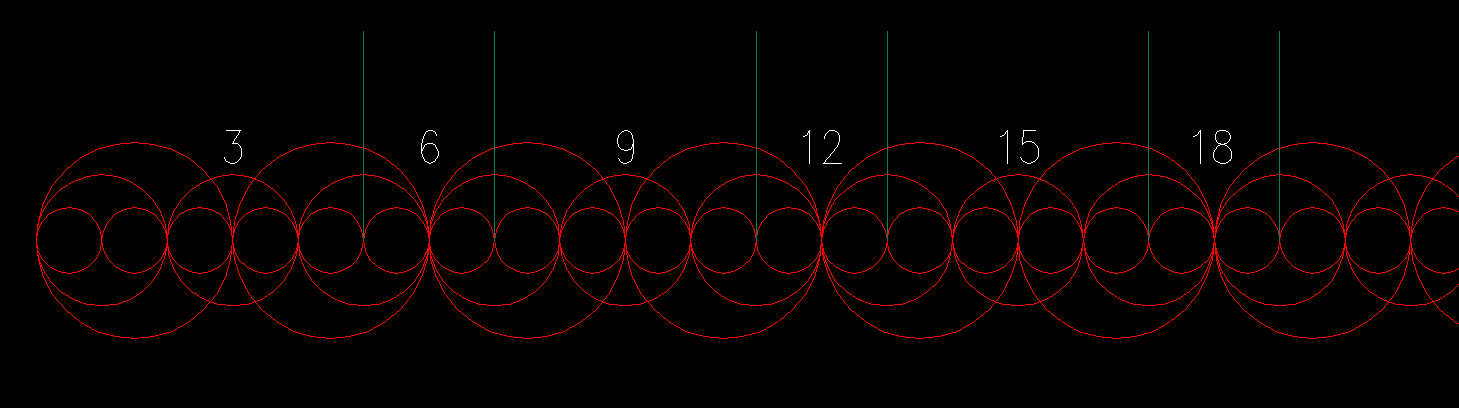
If the only numbers we use are 1, 2 & 3, then we can say that up to the number 18 for example we have 18 / 6 = 3 locations where prime numbers occur. But, at each location you have a pair of primes, so the amount of locations has to be multiplied by two: 18 * 2 / 6 = 18 / 3 = 6. So this approximation says there are 6 primes up to 18, when in fact there are 7.
Now, for larger numbers we need to include more numbers besides 1, 2 & 3. So, I asked myself the following question:
If I assume there are X / 3 prime numbers up to the number X, at what rate are the "excess primes" killed by multiples of prime numbers larger than 3?
Well, I initially wrote the following series:
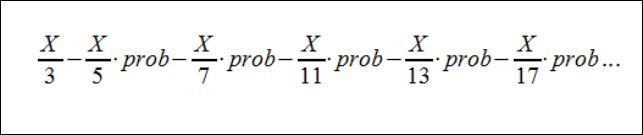
In words, I'm saying the maximum number of primes is X / 3. Then, the number 5 falls on the real axis X / 5 times, so I multiply this by the average probability for multiples of 5 to kill prime numbers in that interval. I apply the same reasoning for 7, 11, 13, 17 and so on for all prime numbers up to the square root of X.
My quest is to find "prob". I have a few series, none of them converge at infinity to the actual number of primes. However, I have noticed that using the number "e" in the series, curiously makes it more precise. Maybe this has something to do with Gauss' discovery.
My first instinct was to try "prob = 2 / p" where "p" is the prime number that is dividing X. Doing this would give you the following series:
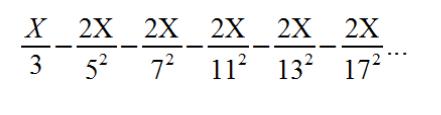
Why 2 / p? well, keeping in mind the tab "A Clockwork Prime" I figured there's always a 2 / p chance of killing possible primes around multiples of 6. Turns out I've been figuring wrong. The series above tends to always overshoot the amount of primes, and the error seems to always grow. I believe the reason for this is that the negative series is converging to the wrong value. This series needs to converge to less than 1/3 at infinity (after factoring out X of course).
Finding "prob" is an interesting quest for me because it could potentially mean that prime numbers have an average and constant probability of falling at 6k +/- 1.
So far, my latest series is problematic because it is divergent, but it counts primes pretty closely up to around 5.000.000, I believe. I will let those who are interested tinker around with the series and the possible alternatives. Remember that the negative series needs to converge to less than 1/3 with x factored out. Anyhow, My latest "divergent" series is:
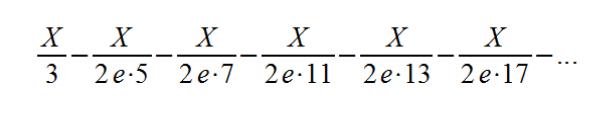
Counting primes is an interesting quest, I still have this particular idea in the back of my head. One thing comes to mind, the series I'm using here seem to be another form of sifting to count primes. I'm not sure it is useful, although the probability concept I think may have some meaning.
I'm hoping to have some more insight into this in the future.